Navigation:  Programmer's Reference >

Retrieving curve fit results from DPlot

 
Previous pageReturn to chapter overviewNext page
Show/Hide Hidden Text

DPlot allows least-squares curve fitting to find the polynomial of a user-specified order that best fits the data. A least-squares curve fit is one in which the sum of the square of the errors between the actual data and the polynomial model are minimized:

 

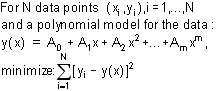
clip0016

 

It is easily possible to retrieve the curve fitting results from DPlot. Here is a step-by-step example:

 

hmtoggle_plus1Create a new document

Doc_num=FNDplot_doc_new(0)      ! create new document

 

hmtoggle_plus1Create the point pairs and store them into a 2D REAL array

Xmin=0

Xmax=2*PI

Xpoints=200

Xstep=Xmax/Xpoints

!

ALLOCATE REAL Datxy(1:Xpoints,1:2)   ! 2-dimensional array

!

RANDOMIZE

Xi=BASE(Datxy,1)

FOR X=Xmin TO Xmax STEP Xstep

   Y1=ATN(X/2)*(X/5+RND*(.1)+RND*.3-1)

  !

   Datxy(Xi,1)=X

   Datxy(Xi,2)=Y1

  IF Xi<Xpoints THEN Xi=Xi+1

NEXT X

 

hmtoggle_plus1Send the point pairs to DPlot

! transfer all data points to DPlot curve 1, line type 1

Dummy=FNDplot_xyz_data(Doc_num,Datxy(*),0,0,1,"y=atn(x/2)*(x/5+RND*(.1)+RND*.3-1)",1)

 

hmtoggle_plus1Some tweaking

Dummy=FNDplot_send_cmd("[SelectCurve(1)]")   ! select curve 1

Dummy=FNDplot_send_cmd("[CurveFit(3)]")     ! curve fitting, order=3 (->new curve 2)

Dummy=FNDplot_send_cmd("[Color(1,0,255,0)]") ! curve 1 = blue

Dummy=FNDplot_send_cmd("[Color(2,255,0,0)]") ! fitted curve 2 = red

Dummy=FNDplot_send_cmd("[NumberFormat(0,8)]")       ! number format for x axis = fractions of PI

Dummy=FNDplot_send_cmd("[NumTicks(1,8)]")           ! number of ticks for x axis

Dummy=FNDplot_send_cmd("[ManualScale(,-1.2,,1.2)]") ! manual scale of y axis

 

hmtoggle_plus1Show  the diagram on the HTBasic screen

! show the diagram, 100% screen size

CALL Dplot_show(Doc_num)

 

.. which should give the following result (curve 1 = blue, fitted curve 2 = red):

clip0052

 

hmtoggle_plus1Get back the curve fitting results from DPlot

DIM Lastcurvefit$[1024],Crlf$[10]

Crlf$=CHR$(10)&CHR$(13)

Lastcurvefit$=FNDplot_request$("","LastCurveFit")

IF Lastcurvefit$<>"" THEN

  IF Verb_=1 THEN

      OUTPUT CRT;"     * Last curve fit results:"&Crlf$&Lastcurvefit$

  END IF

END IF

 

The variable Lastcurvefit$ now contains the following text:

y = C(0) + C(1)*x + C(2)*x^2 + ...

Coefficients

C(00) = -0.0187877640693

C(01) = -0.370005452219

C(02) = 0.132414224948

C(03) = -0.00968681409756

 

Correlation coefficient is 0.94777033888

 

hmtoggle_plus1Close the DPlot document

Dummy=FNDplot_doc_close(Doc_num)     ! close the document

 

 

lampe

Hint: è Example program 1 demonstrates how to retrieve data points from DPlot curves

(see SUB DPlot_xygraph).